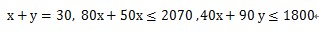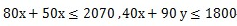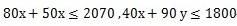【导读】华图国家公务员考试网同步未知发布:2014年国考运算思路:一题多解,更多关于2014年国考的内容请关注广西国家公务员考试网,以及广西华图微信公众号(gxhuatu)和国考交流群:175995961),获取更多招考信息和备考资料。
在去年年国考数学运算中有一道不等式的题,不等式的问题是数量关系中的难点,华图公务员考试研究中心希望可以通过这道题对不等式问题有所思考。
【例题】某市园林部门计划对市区内30处绿化带进行补栽,每处绿化带补栽方案可从甲、乙两种方案中任选其中一方案进行。甲方案补栽阔叶树80株,针叶树40株:乙方案补栽阔叶树50株,针叶树90株。现有阔叶树苗2070株,针叶树苗1800株,为最大限度利用这批树苗,甲、乙两种方案应各选:
A.甲方案19个、乙方案11个 B.甲方案20个、乙方案10个
C.甲方案17个、乙方案13个 D.甲方案18个,乙方案12个
这道题是要求最大利用树苗,就是剩下的树苗数目最少。我们可以把题目转换为:设甲方案选x件,乙方案选y件
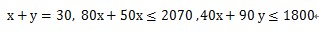
要求的是所剩树苗2070-(80x+50y)+1800-(40x+90y)的值最小。
代入排除
首先我们可以想到是代入法,这种方法是思路最简单的方法。我们把选项的值带入所求的2070-(80x+50y)+1800-(40x+90y)中,看看哪个值是最小的。
|
x |
y |
2070-(80x+50y)+1800-(40x+90y) |
|
17 |
13 |
10 |
|
18 |
12 |
30 |
|
19 |
11 |
50 |
|
20 |
10 |
70 |
这样看来好像应该选择x=17,y=13使得所剩树苗数目最小。但是我们忽略一个限制条件:
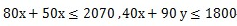
所以我们还需要把选项带入这两个条件中验证是否符合:
|
x |
y |
2070 >(80x+50y) |
1800 > (40x+90y) |
|
17 |
13 |
符合 |
不符合 |
|
18 |
12 |
符合 |
符合 |
|
19 |
11 |
符合 |
符合 |
|
20 |
10 |
不符合 |
符合 |
这样看来只有两个选项符合我们的要求,我们从中选择使2070-(80x+50y)+1800-(40x+90y)最小的,即x=18,y=12.
解不等式
不等式原则上是可以求解的,但是一般我们不提倡这样,因为计算量较大并且容易得到错误的结果,不过我们为了更好理解不等式题目,有必要把不等式解法给大家介绍一下。
解不等式方程
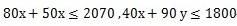
需要把这两个函数画出来,得到:
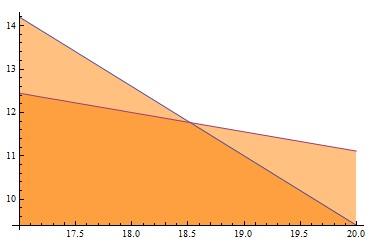
符合不等式限制的区域只有最下面深色区域,在这个区域的整数点只有(19,11),(19,10),,,(18,12)(18,11)(18,10),,,(17,12)(17,11),,,,符合x+y=30条件的点只有(19,11)和(18,12),我们只有在这两个候选点中进行选择,带入题干验证哪种选择使所剩树苗最少。
解方程
这里我想介绍一种用解方程代替解不等式方程的方法,既然约束条件是
并且要求不等式左右相差尽量的小,那么我们把这个式子看做一个等式试试解一下。解方程组80x+50y=2070和40x+90y=1800得到x=18.5,y=11.8 。我们选择符合x+y=30并且最靠近(18.5,11.8)的整数点(18,12)即我们所要求的答案。
这种方法简答但是不严格,但在限制时间做题过程中不失为猜想答案的好方法。
以上为2014年国考运算思路:一题多解的内容,更多关于2014年国考的信息请关注广西国家公务员考试网/广西人事考试网。
本文地址:https://gx.huatu.com/2013/0906/716723.html
(编辑:网易号后台)